June 19, 8:30-09:00 – Registration
June 19, 9:00-18:00 – Scientific Program
June 19, 19:00 – Cocktail-buffet
Scientific Program (amphitheater C):
9:00 – 10:00 Opening and Keynote I
Chair: Matthias Ehrgott (University of Lancaster, UK)
09:00 – 09:10: Xavier Gandibleux (Université de Nantes) and Michel Malabre (CNRS)
09:10 – 10:00: Serpil Sayın (Koç University. Istanbul, Turkey). Exact and Representation Methods in Multiobjective Optimization. Joint work with Gökhan Kirlik (University of Maryland).
(Abstract)
We present an algorithm that generates all nondominated solutions for multiobjective discrete optimization problems with p objective functions. The algorithm conducts a search in the (p − 1)-dimensional space and utilizes rectangles in the process. We then discuss if representations with quality guarantees may be considered as exact solutions and explore the consequences in discrete and continuous problems. We outline a general methodological framework for finding representations with quality guarantees that applies to continuous problems as well.
10:00 – 10:10 Break
10:10 – 11:25 Session 1 – Enumeration methods (I) and combinatorial optimization
Chair: Sophie Parragh (University of Vienna, Austria)
10:10 – 10:35: Lucie Galand (Université Paris-Dauphine, France). Determination of best compromise solutions by ranking algorithms: application to the multi-objective assignment problem. Joint work with Lyes Belhoul (Université Paris-Dauphine) and Daniel Vanderpooten (Université Paris-Dauphine).
(Abstract)
A best compromise solution to a multi-objective optimization problem optimizes a scalarizing function (e.g. a weighted Tchebychev norm). In multi-objective combinatorial optimization, such a solution can be determined by resorting to a ranking (or k-best) algorithm that enumerates feasible solutions according to an appropriate weighted sum until a valid stopping condition is met. In this talk we show how this method can be efficiently applied to the multiobjective assignment problem.
10:35 – 11:00: Audrey Cerqueus (Université de Nantes, France). A branch-and-cut method for the bi-objective bi-dimensional knapsack problem. Joint work with Xavier Gandibleux (Université de Nantes), Anthony Przybylski (Université de Nantes), Stefan Ruzika (Universität Koblenz-Landau), Frédéric Saubion (Université d’Angers).
(Abstract)
This work presents a branch-and-cut method to solve exactly the bi-objective bi-dimensional knapsack problem. Its main component is the generation of valid inequalities forbiding a set of incompatible items. We will describe the different mechanisms of our branch-and-cut (separation procedure, bound sets, generation of valid inequalities…) and experimentally validate them.
11:00 – 11:25: Thomas Stidsen (Technical University of Denmark, Denmark). Optimized Parallel Branch & Cut algorithm for Bi-Objective TSP. Joint work with Kim Allan Andersen (Aarhus University).
(Abstract)
The bi-objective Travelling Salesman Problem (BI-TSP) is solved using a three step procedure: Heuristic solution, division into independent BI-TSP problems, solution of independent BI-TSP problems. Through optimized BI-TSP division, it becomes possible to solve BI-TSP problems of significant size.
11:25 – 11:40 Coffee Break
11:40 – 12:40 Session 2 – Representation and vector optimization
Chair: Ivana Ljubic (University of Vienna, Austria)
11:40 – 12:10: Renaud Lacour (Bergische Universität Wuppertal, Germany). On the representation of the search region in multi-objective optimization. Joint work with Kerstin Dächert (University of Duisburg-Essen), Kathrin Klamroth (Bergische Universität Wuppertal), Daniel Vanderpooten (Université Paris-Dauphine).
(Abstract)
In this talk, we investigate the representation of the search region of a multi-objective optimization problem through local upper bounds (in the minimization case). Given a set of feasible points, the search region is the part of the objective space that none of these points dominate. We study properties of this representation and present and compare several approaches for its computation.
12:10 – 12:40: Andreas Löhne (Martin-Luther-Universität Halle-Wittenberg, Germany). BENSOLVE – a solver for vector linear programs. Joint work with Benjamin Weißing (Martin-Luther-Universität Halle-Wittenberg).
(Abstract)
BENSOLVE is a free and open source implementation on Benson’s algorithm and its extensions. From version 2 it is written in C programming language and published under the GPL license. The talk surveys the theoretical background and outlines the usage of the software. Numerical examples are presented.
12:40 – 12:50 Some Information
12:50 – 14:00 Lunch Break
14:00 – 15:30 Session 3 – Enumeration methods (II) and applications
Chair: Daniel Vanderpooten (University Paris-Dauphine, France)
14:00 – 14:30: Markus Sinnl (University of Vienna, Austria). A new exact method and matheuristics for bi-objective 0/1 ILPs: Application to FTTx-network design. Joint work with Markus Leitner (University of Vienna), Ivana Ljubic (University of Vienna) and Axel Werner (ZIB Berlin).
(Abstract)
In this talk, we focus on bi-objective 0/1 ILPs and propose a new exact method, adaptive search in objective space. In addition, two matheuristics, boundary induced neighborhood search and directional local branching are introduced. Finally, a two-phase ILP-based heuristic framework relying on the two matheuristics is presented. Our new methods are computationally evaluated on two problems of particular relevance for the design of FTTx-networks.
14:30 – 15:00: Walter Gutjahr (University of Vienna, Austria). Bi-objective Bilevel Optimization of Facility Locations Considering User Equilibria. Joint work with Nada Dzubur (TU Wien).
(Abstract)
A bi-objective, bilevel optimization model for the location of distribution centers (DCs) under limited supply is proposed. The upper-level decision maker selects locations for capacitated DCs with objectives cost and uncovered demand. On the lower level, customers choose DCs according to distance and amount of supply to be expected, which leads to a user equilibrium. We compute the exact Pareto frontier, using the adaptive epsilon-constraint method, a branch-and-bound procedure, and the Frank-Wolfe algorithm.
15:00 – 15:30: Joan Davins-Valldaura (Renault and Ecole Centrale Nantes, France). Multi-objective optimization for tuning driver assistance systems using large databases. Joint work with Saïd Moussaoui (Ecole Centrale Nantes), Guillermo Pita-Gil (Renault) and Franck Plestan (Ecole Centrale Nantes).
(Abstract)
A lot of engineering applications include multi-objective optimization in the case of black-box expensive objective functions. The main purpose is to find a set of optimal solutions in a limited global processing time. We propose an extension of the ParEGO (Pareto Efficient Global Optimization) algorithm for finding the Pareto Front by introducing a double Kriging strategy allowing to calculate a modified expected improvement criterion that jointly accounts for the objective function approximation error and the probability to find Pareto Set solutions. This algorithm was used for the automatic setting an indirect tyre pressure monitoring system.
15:30 – 15:50 Coffee Break
15:50 – 16:50 Session 4 – Interval Methods
Chair: Alexandre Goldsztejn (CNRS)
15:50 – 16:20: Boglárka G.-Tóth (Budapest University of Technology and Economics, Hungary). Biobjective Interval Methods. Joint work with José Fernández (University of Murcia).
(Abstract)
In this talk general reliable methods for biobjective optimization are shown with accelerating devices, which can be applied to any continuous optimization problem. The methods are based on the interval branch and bound algorithm for uniobjective optimization. To prove the applicability of the methods, several competitive facility location problems have been solved with them.
16:20 – 16:50: Benjamin Martin (Universidade Nova de Lisboa, Portugal). Interval Branch & Bound with constraint programming techniques for non-linear bi-objective optimization. Joint work with Alexandre Goldsztejn (CNRS), Laurent Granvilliers (Université de Nantes) and Christophe Jermann (Université de Nantes).
(Abstract)
The use of constraint programming techniques such as constraint propagation has helped to improve the convergence of Branch & Bound methods in non-linear optimization. In this talk, we present a general constraint-based Branch & Bound algorithm for solving non-linear bi-objective optimization problems. Noticeably, it generalizes the different approaches from the literature and includes efficient pruning techniques. In particular, it uses a constraint propagation method that exploits the upper bound set with dominance contractors. The performance of this new approach is assessed on a set of bi-objective benchmark problems.
16:50 – 17:00 Break
17:00 – 18:00 Keynote II and Closing
Chair: Anthony Przybylski (University of Nantes, France)
17:00 – 17:50: Stefan Ruzika (Universität Koblenz-Landau. Koblenz, Germany). Why would you ever „vectorize“ a single objective optimization problem?
(Abstract)
It goes without saying that vector-valued optimization problems are considered to be in general more difficult than scalar-valued optimization problems. Would it ever make sense to artificially “vectorize” a scalar-valued optimization problem? In this talk, I want to show two important and convincing cases which demonstrate that a “vector-valued optimization“-perspective can provide new ideas for solving scalar-valued combinatorial optimization problems. In both cases, the problems are NP-hard, i.e., they belong to the class of problems which is considered difficult.
The first case is about the exact solution of some combinatorial optimization problems that are subject to a knapsack-type side constraint. Problems of this kind are very common and therefore important since they appear in applications and as subproblems in more complex models. This case is motivated by mathematical programming decoding (i.e., by designing decoding algorithms based on ideas from mathematical programming) and the solution techniques are illustrated using the constrained minimum spanning tree problem.
The second case is motivated by a special kind of network flow problem, the so-called robust quickest path problem, which has applications in evacuation planning. For this path problem, a fully polynomial time approximation scheme is developed using ideas from vector-valued optimization. Asking for robust solutions is especially important in practice since decision makers often face the problem that one scenario out of a set of possible scenarios might occur but it is not known in advance which scenario it is.
19:00 – Cocktail-buffet
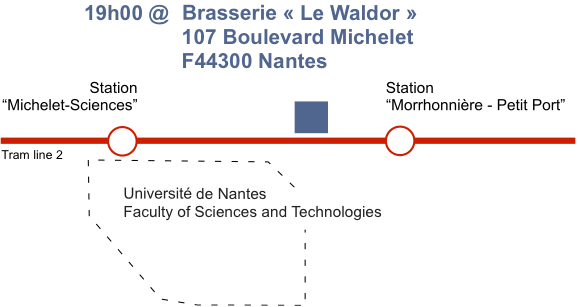
For the participants who received a ticket (i.e. attendees who are not affiliated to an institution located in Nantes), you are invited to reach us for a cocktail-buffet Friday evening.
• Where: Brasserie « Le Waldor ». 107 Boulevard Michelet, 44300 Nantes
• Access: Tram station « Michelet-Sciences » or « Morrhonnière – Petit Port »
• Map: